Оскільки у педагогічному процесі більшість явищ взаємообумовлені і взаємопов'язані, то дослідникам часто доводиться встановлювати наявність або відсутність зв'язку між досліджуваними параметрами, використовуючи коефіцієнти кореляції. Метод кореляції допомагає з високою ймовірністю стверджувати наявність зв'язку між параметрами. Зокрема, можна встановити залежність успішності учнів із навчального предмету від розвитку їхньої пізнавальної активності, спостережливості або загальнонавчальних умінь.
Для інтервальних шкал застосовують лінійну кореляцію (за К. Пірсоном), а для порядкових і невеликих вибірок - порядкову, або рангову кореляцію (за Спірменом).
Отриманий емпіричний коефіцієнт лінійної кореляції (remp) слід порівняти з його табличним значенням (rkrit) (див. табл. 3.13), у якій подані 95% і 99 % ймовірності та n - кількість пар, що порівнюються.
Якщо ІrempІ ? rkrit, то існує зв'язок між двома досліджуваними явищами. Причому чим більша різниця між remp і rkrit тим сильнішим цей зв'язок. Якщо remp має знак "-" то зв'язок між явищами, що досліджуються є оберненим, якщо remp "+" - зв'язок прямий.
Коли ІrempІ < rkrit, то лінійний зв'язок між двома досліджуваними параметрами відсутній.
Порядкова, або рангова кореляція
(за Спірменом)
Порядкову кореляцію можна застосовувати не тільки для порядкових, але й для інтервальних шкал.
Обчислюється коефіцієнт порядкової кореляції (р) за формулою:
Ранги значень знаходять таким чином:
1) розташовують значення у висхідному (або низхідному) порядку;
2) кожному значенню приписується ранг. Ранг - це порядковий номер (місце) конкретного значення у впорядкованому ряді;
3) якщо два учні (або більше) отримали однакові значення, то рангом буде для цих значень середнє арифметичне їхніх порядкових номерів (місць) у ряді. Наприклад, проранжуємо таку сукупність оцінок учнів з навчального предмету: 7, 8, 8,6, 5, 8, 8, 10. Розмістимо ці дані у табл. 3.14.
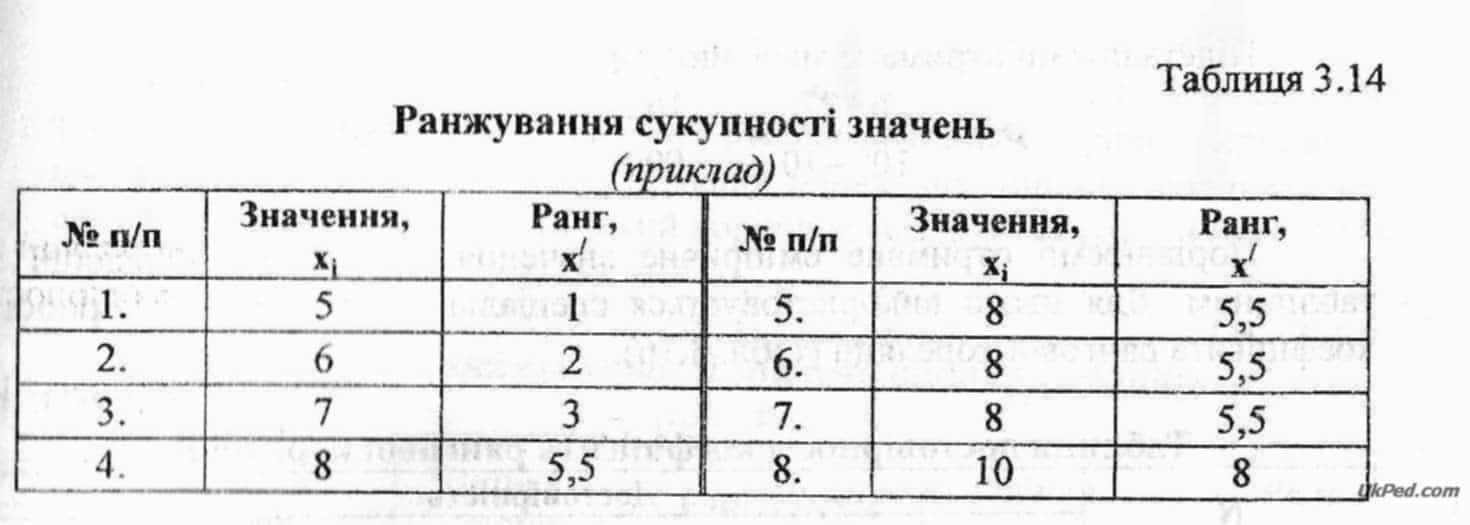
Значення 8 займає 4, 5, 6 і 7 місця у ряді, тому його ранг буде середнє арифметичне номерів цих місць: (4+5+6+7):4 = 5,5. Числу 10 приписується ранг - 8.
Перевірка правильності ранжування: останній ранг дорівнює загальній кількості значень у сукупності (у нашому випадку останній ранг - 8).
Підрахунок коефіцієнта рангової кореляції.
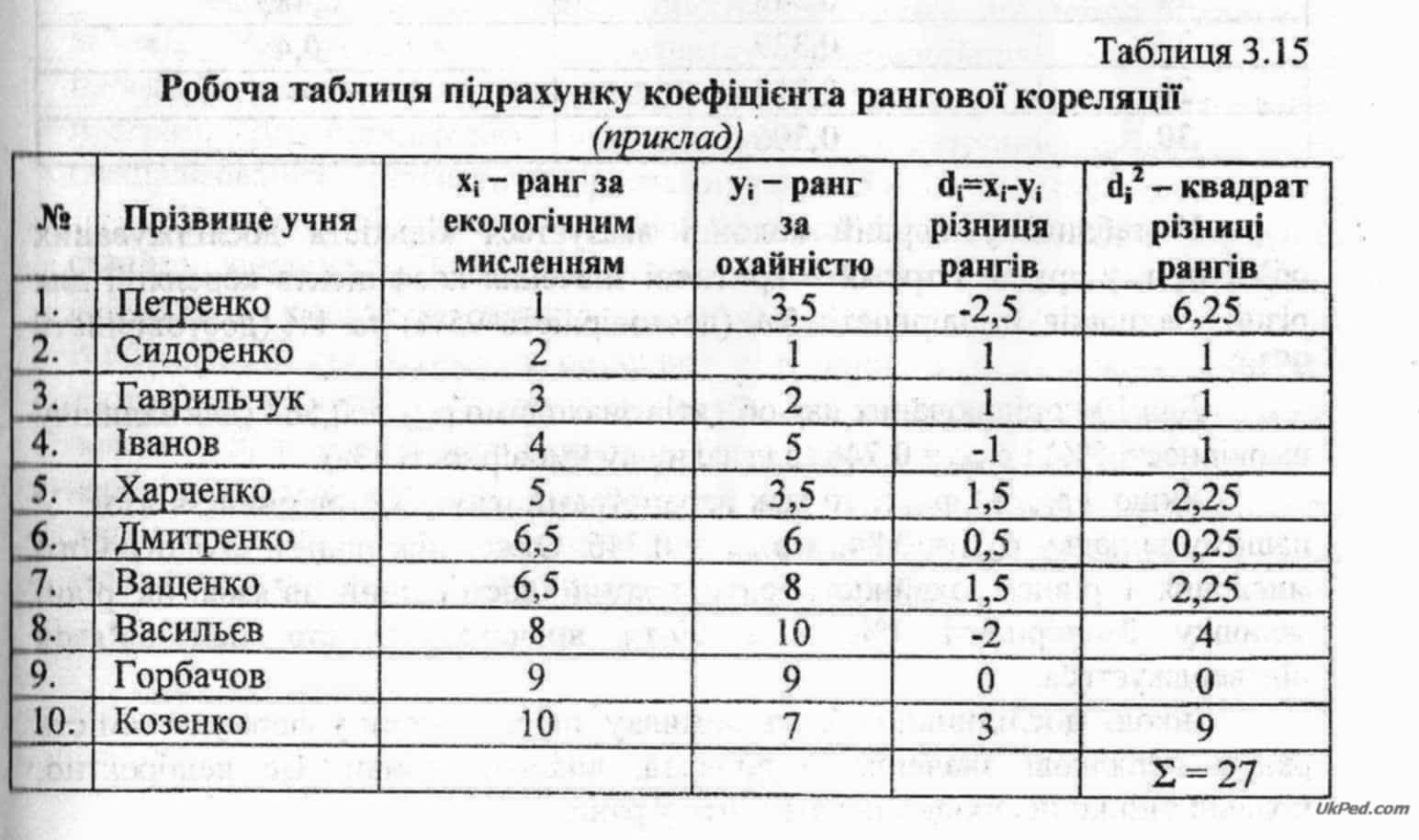
Наприклад, необхідно встановити, чи існує достовірний зв'язок між екологічним мисленням учнів та їх охайністю.
1. Для цього учнів класу ранжують за показником рівня екологічного мислення.
2. Потім їх ранжують за рівнем охайності.
3. Далі знаходять різницю рангів для кожного учня між рівнем екологічного мислення та рівнем охайності.
4. Підносять кожну різницю до квадрату і додають (знаходять суму).
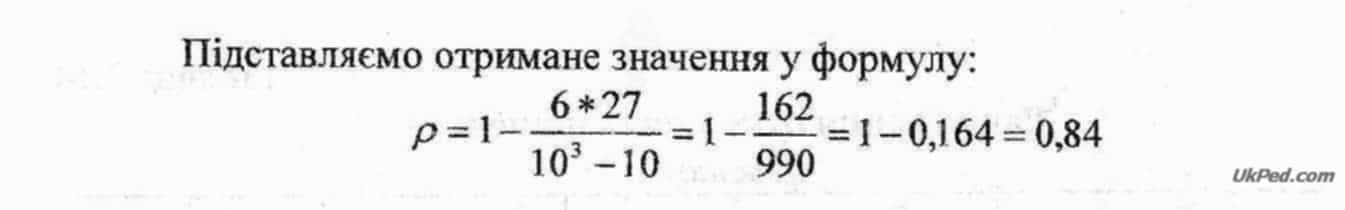
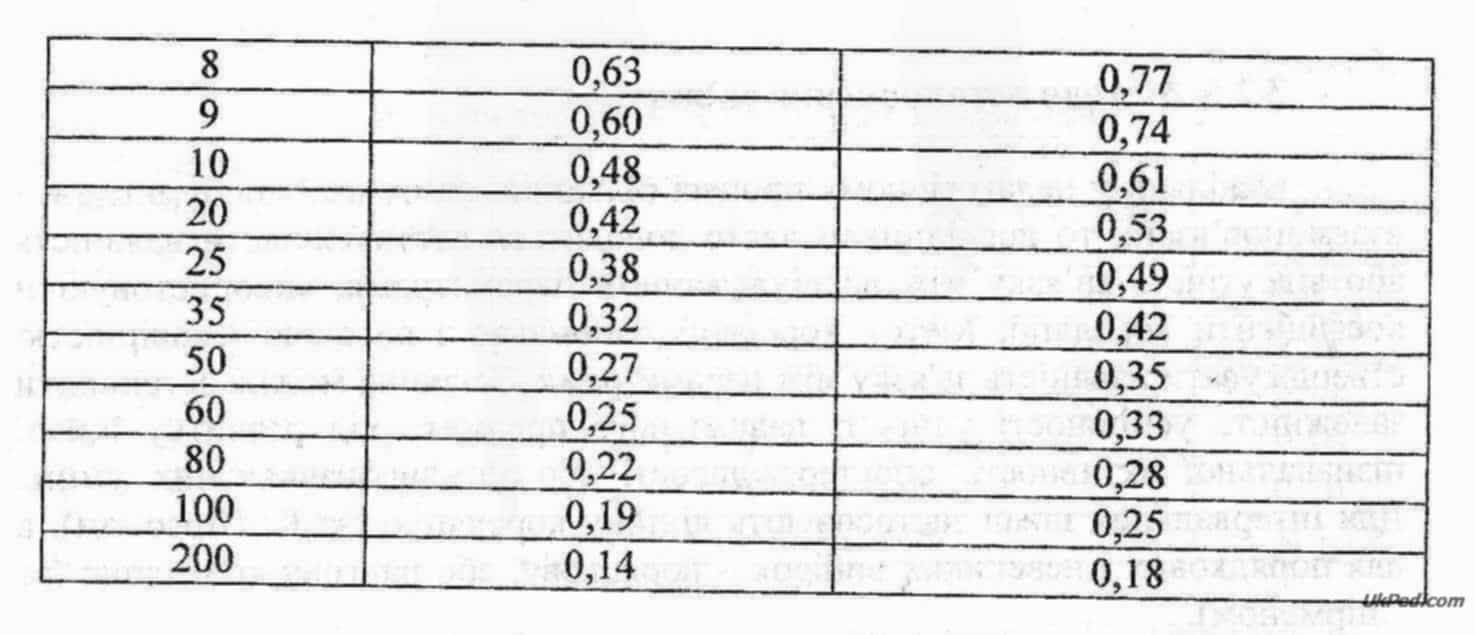
Порівнюємо отримане емпіричне значення коефіцієнта кореляції з табличним. Для цього використовується спеціальна таблиця достовірності коефіцієнта рангової кореляції (табл. 3.16).
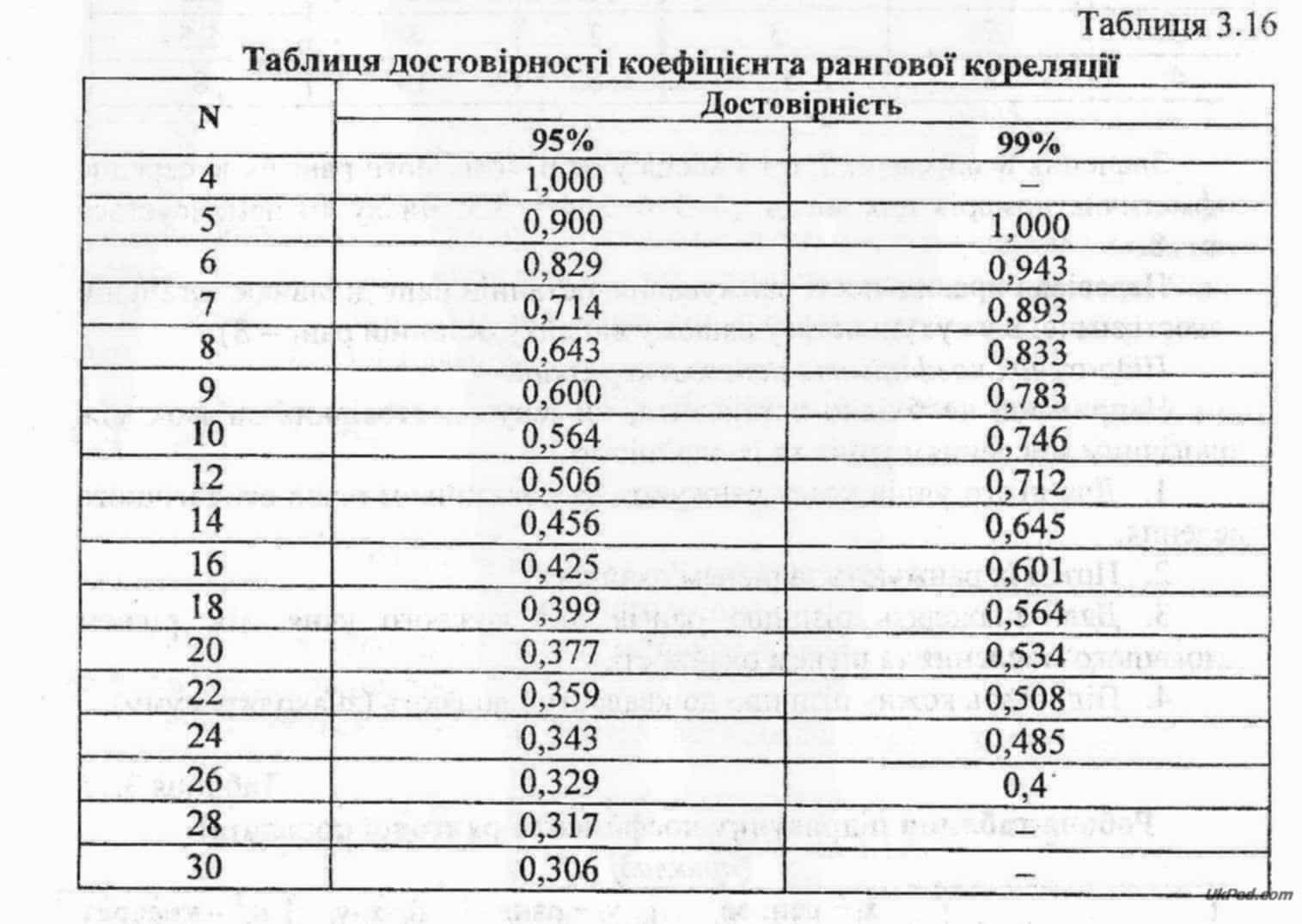
У таблиці у першій колонці вказується кількість досліджуваних об'єктів п, у другій і третій - критичні значення коефіцієнта кореляції для різних залишків ймовірності: 5% (достовірність 95%) та 1%.(достовірність 99%)
Для 10 порівнюваних пар об'єктів знаходимо ртабл. = 0,564 (для залишку ймовірності 5%) і ртабл. = 0,746 (для залишку ймовірності 1%).
Якщо Іремп.І > ртабл., то між параметрами існує достовірний зв'язок. У нашому випадку ремп. = 0,84, а ртабл. = 0,746. Отже, між рівнем екологічного мислення і рівнем охайності існує прямий достовірний зв'язок на рівні залишку ймовірності 1%, і в 99-ти випадках із ста цей зв'язок підтверджується.
Інколи дослідники роблять помилку, підставляючи у формулу замість рангів порядкові значення, наприклад, шкільні оцінки. Це некоректно, шкільні оцінки необхідно перетворити у ранги.
Наприклад, необхідно встановити характер зв'язку між оцінками учнів з української мови і математики. Переводимо оцінки у ранги, приписуючи перший ранг найвищій оцінці. Якщо однакових оцінок декілька, то їм приписується однаковий ранг, який дорівнює середньому рангу (табл. 3.17).
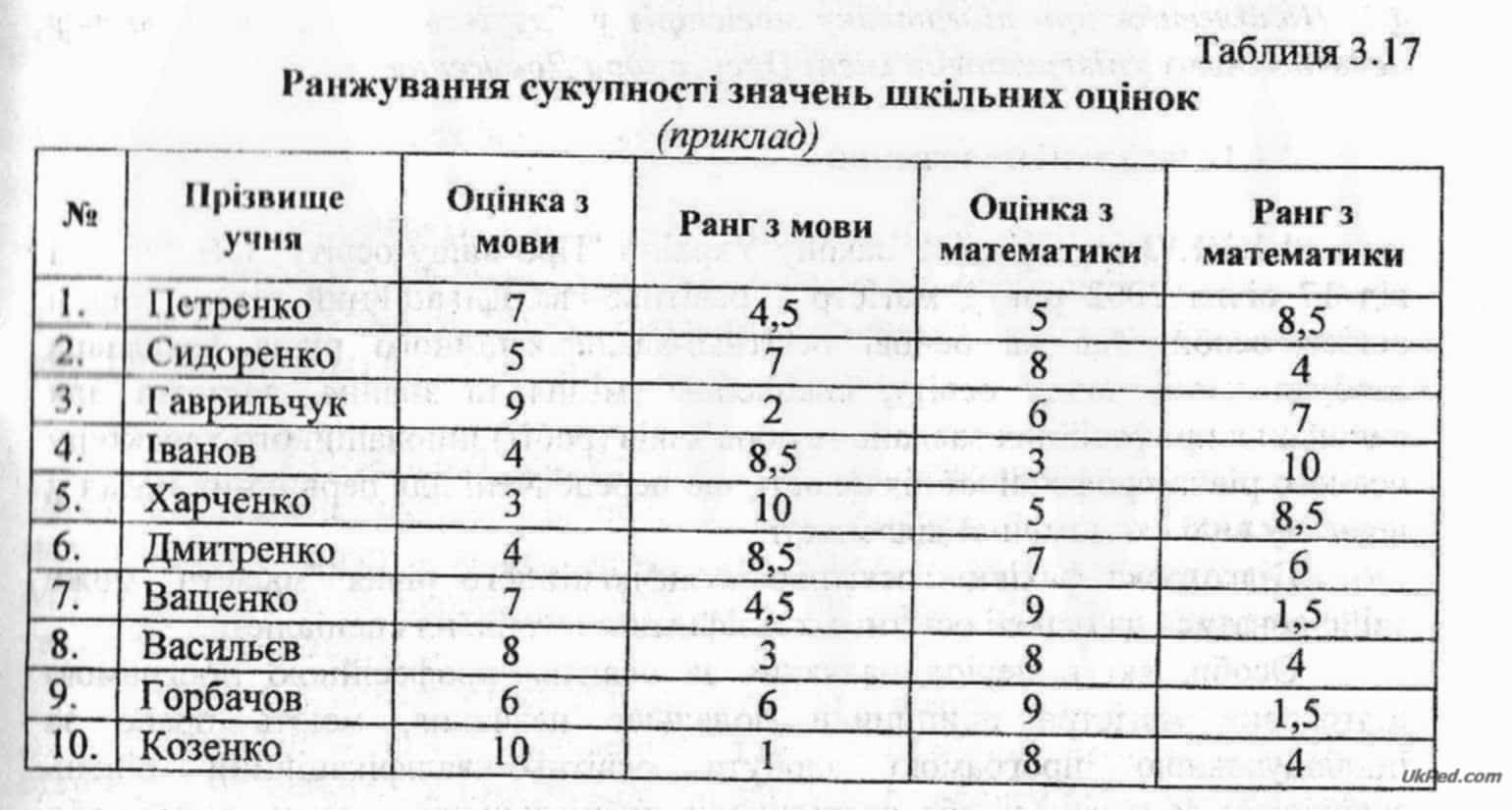
Далі всі дії щодо встановлення зв'язку проводяться з рангами аналогічно попередньому прикладу.
Наведені приклади тільки пояснюють схему дій щодо підрахунку зв'язків. На сучасному етапі розвитку інформаційних технологій дана процедура виконується швидко з допомогою стандартних та спеціальних програм. До стандартних можна віднести електронні таблиці, а до спеціалізованих - статистичні програми Sratgraft OSA, Statisticf тощо.
У педагогіці шляхи досягнення мети навчання і виховання формують складні системи. Для констатації педагогічних явищ застосовують найчастіше емпіричні методи дослідження (спостереження, тестування тощо). Проте статистика не розкриває суті явищ, а лише фіксує факт або достовірну різницю між двома явищами, що досліджуються, але не може пояснити причини цих розбіжностей. Тому поряд з кількісним аналізом явищ необхідно здійснювати і якісний, що ґрунтується глибокому вивченні досліджуваного процесу, всебічному спостереженні за об'єктами, умінні знаходити й пояснювати причинно-наслідкові зв'язки.
Лівінський О.М., Курок О.І., Гридякін В.О., Зінченко В.П.
Методологія і методи наукових досліджень
Навчальний посібник