Проблема формування професійної компетентності в будь-якій галузі знаходиться в полі зору багатьох наукових дисциплін: соціології, історії, філософії, культурології, педагогіки, психології, предметних методик.
Під професійною компетентністю педагога розуміють особистісні можливості вчителя, які дають йому змогу самостійно й ефективно реалізовувати цілі педагогічного процесу. В умовах реалізації національної концепції навчання і виховання школярів висуваються нові вимоги до професійної компетентності вчителів початкової школи, оскільки вони найперші залучаються до формування громадян нової генерації.
Підвищення якості математичної освіти — актуальна проблема не тільки для України, а й для всієї світової спільноти. Одним із ефективних шляхів оновлення змісту освіти й навчальних технологій, узгодження їх із сучасними потребами, інтегрування у світовий освітній простір є орієнтація освіти на компетентнісний підхід і створення ефективних механізмів його запровадження.
Реформування початкової математичної освіти в Україні є частиною процесу модернізації освітньої системи. Ці зміни стосуються створення нових освітніх стандартів, оновлення і перегляду навчальних програм, змісту навчально-дидактичних матеріалів, підручників, створення сучасних засобів навчання.
Формування у школярів ключових і предметних компетентностей значною мірою залежить від рівня як математичної, так і методичної підготовки вчителя початкових класів.
У новій редакції "Навчальних програм для загальноосвітніх навчальних закладів" зазначено, що важливу роль у формуванні компетентності учня відіграє розвиток здатності розпізнавати практичні проблеми, які можна вирішувати із застосуванням математичних методів. З огляду на це особливо значущу роль відведено в курсі навчання математики змістовій лінії "Сюжетні задачі". Метою цієї змістової лінії є формування в учнів загального вміння працювати над задачею, розв'язувати задачі певних видів.
У новій редакції "Навчальних програм для загальноосвітніх навчальних закладів" зазначено, що важливу роль у формуванні компетентності учня відіграє розвиток здатності розпізнавати практичні проблеми, які можна вирішувати із застосуванням математичних методів. З огляду на це особливо значущу роль відведено в курсі навчання математики змістовій лінії "Сюжетні задачі". Метою цієї змістової лінії є формування в учнів загального вміння працювати над задачею, розв'язувати задачі певних видів.
Під математичною задачею розуміють будь-яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ. Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин й існує залежність, яка пов'язує ці величини як між собою, так і з шуканою.
Задачі в початковому курсі математики, з одного боку, становлять специфічний розділ програми, який мають засвоїти учні, а з другого — виступають як дидактичний засіб навчання, виховання і розвитку школярів. Отже, задачі мають як навчальні, так і виховні та розвивальні функції.
Навчальні функції задач спрямовані на формування системи математичних знань, умінь і навичок на різних етапах її засвоєння. Початкове розкриття змісту арифметичних дій здійснюється за допомогою відповідних операцій над предметними множинами.
Навчальні функції задач виявляються також у процесі контролю знань і математичного розвитку учнів. Самостійне розв'язування задач як засіб оберненого зв'язку (учень — учитель) дає змогу виявляти вміння правильно обирати і виконувати арифметичні дії, робити висновок про розвиток мислення школярів.
Виховні функції задач сприяють органічним зв'язкам навчання з життям, виховують у дітей сві¬доме ставлення до навчання, бажання зробити власний внесок у загальну справу. Внутрішня краса самої математики, оригінальність прийомів розв'язання задач збуджують у дітей естетичні почуття.
Під розвивальними розуміють функції задач, спрямовані на формування в учнів науково-теоретичного, зокрема функціонального стилю мислення, на оволодіння цими прийомами розумової діяльності.
На формування і розвиток умінь молодших школярів розв'язувати задачі відводиться 40-50% часу, передбаченого на вивчення математики. Задачі розв'язують на кожному уроці і виділяють на це 15-20 хв.
Надзвичайно важливу роль у навчанні молодших школярів відіграють прості задачі. Уміння їх розв'язувати є фундаментом умінь розв'язувати складені задачі, які є ланцюгами простих. На простих задачах учитель ознайомлює учнів з їх структурою, основними прийомами роботи з ними, формує різні математичні поняття, зокрема поняття про арифметичні дії.
Навчити учнів розв'язувати задачі — означає навчити їх розкривати зв'язки між даними і шуканими значеннями величин; на основі чого вибирати, а потім виконувати арифметичні дії. Від того, наскільки добре розуміють учні зміст зв'язків, залежить їхнє уміння розв'язувати прості задачі.
Залежно від цих зв'язків прості задачі поділяють на.4 групи (задачі одного виду):
На формування і розвиток умінь молодших школярів розв'язувати задачі відводиться 40-50% часу, передбаченого на вивчення математики. Задачі розв'язують на кожному уроці і виділяють на це 15-20 хв.
Надзвичайно важливу роль у навчанні молодших школярів відіграють прості задачі. Уміння їх розв'язувати є фундаментом умінь розв'язувати складені задачі, які є ланцюгами простих. На простих задачах учитель ознайомлює учнів з їх структурою, основними прийомами роботи з ними, формує різні математичні поняття, зокрема поняття про арифметичні дії.
Навчити учнів розв'язувати задачі — означає навчити їх розкривати зв'язки між даними і шуканими значеннями величин; на основі чого вибирати, а потім виконувати арифметичні дії. Від того, наскільки добре розуміють учні зміст зв'язків, залежить їхнє уміння розв'язувати прості задачі.
Залежно від цих зв'язків прості задачі поділяють на.4 групи (задачі одного виду):
- 1 група. Задачі, які розкривають конкретний зміст арифметичних дій (на знаходження суми, остачі, добутку, частки).
- 2 група. Задачі на знаходження невідомого компонента арифметичної дії (на знаходження невідомого доданка, зменшуваного, від'ємника, множника, діленого, дільника).
- 3 група. Задачі на різницеве і кратне порівняння із запитаннями: "На скільки більше (менше)?", "У скільки разів більше (менше)?".
- 4 група. Задачі на збільшення (зменшення) числа на кілька одиниць у прямій і непрямій формі. Задачі на збільшення (зменшення) числа у кілька разів у прямій і непрямій формі.
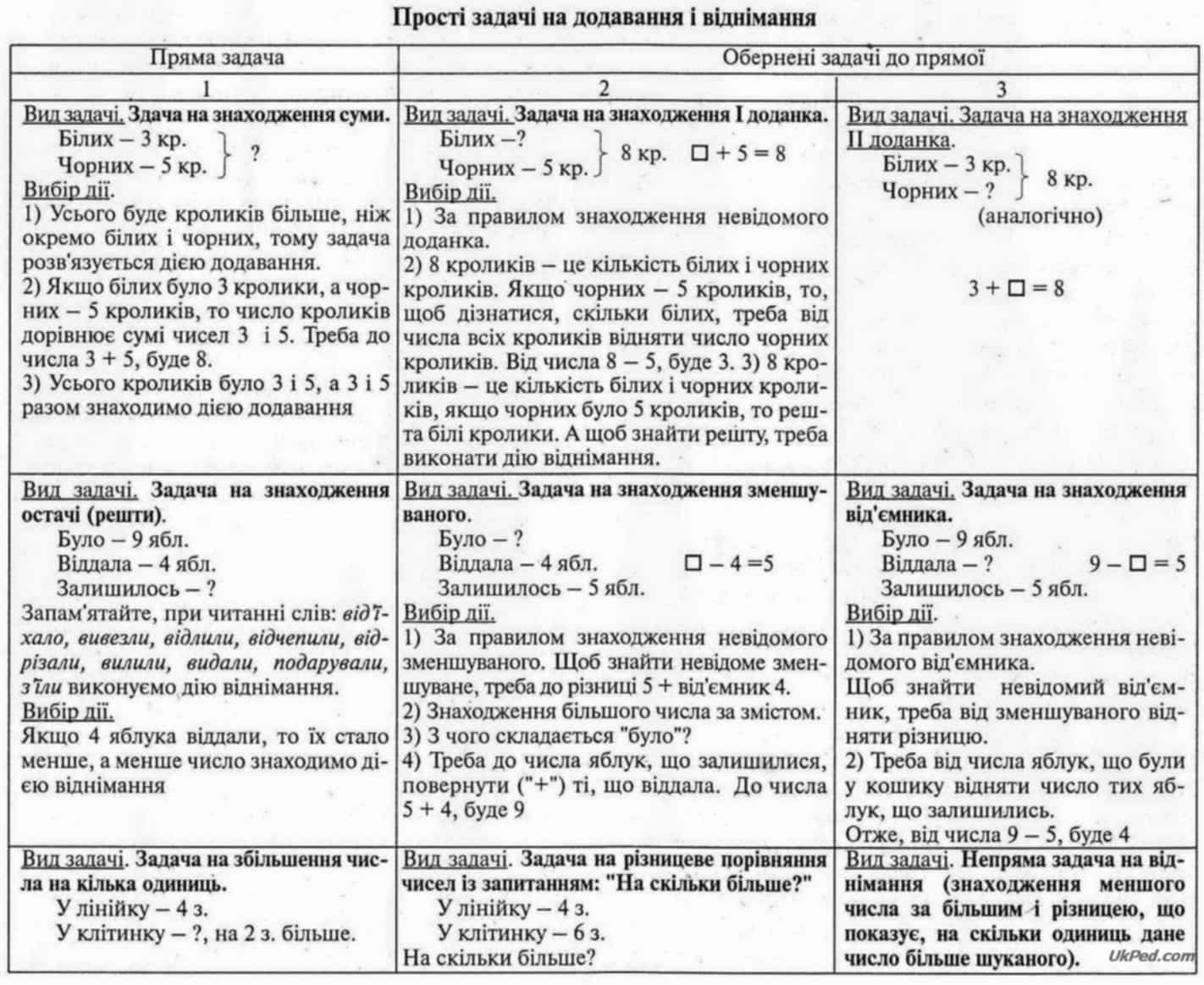
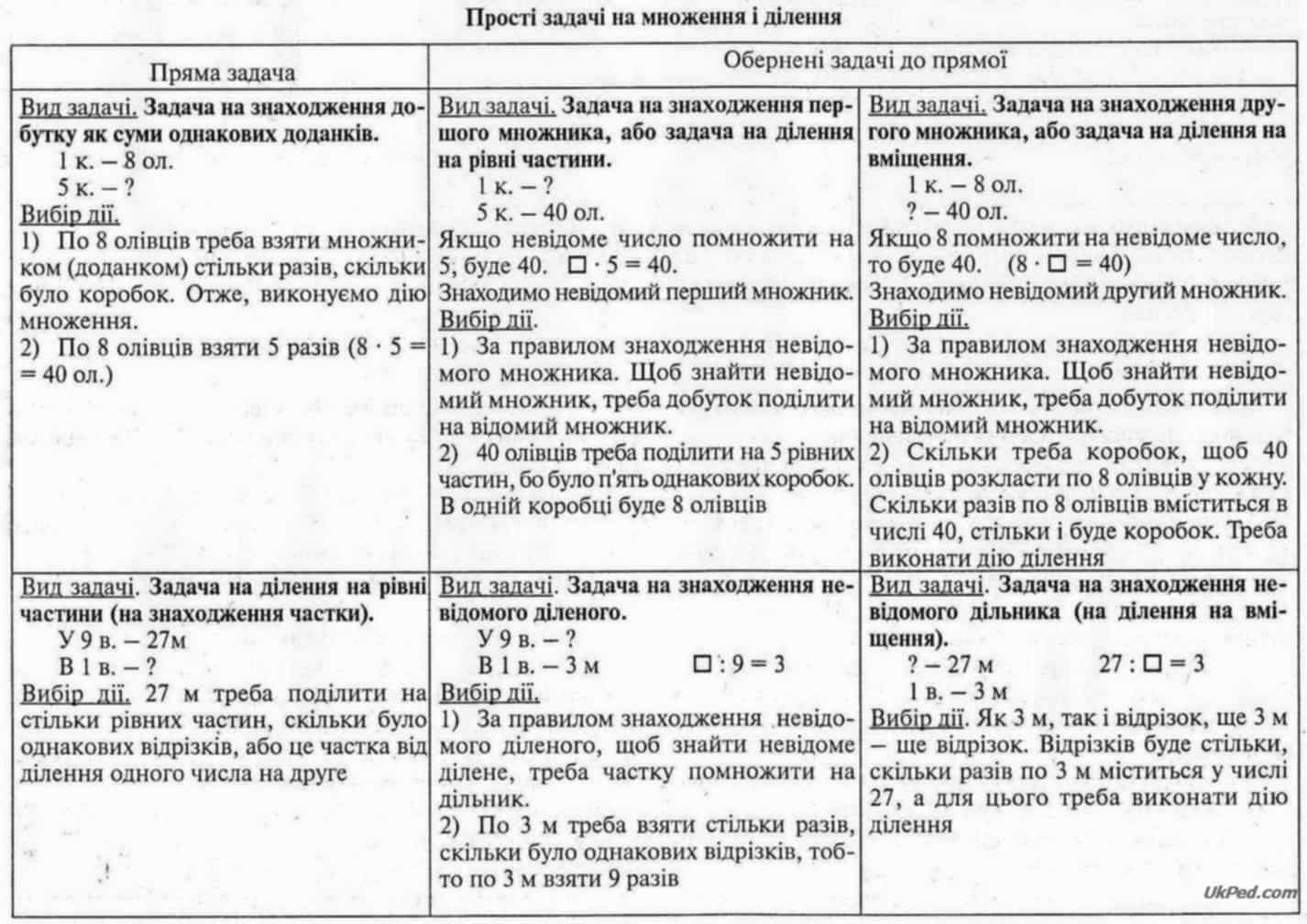
Пропонуємо таблицю простих задач на додавання, віднімання, множення, ділення та обернених до них.
У наведених схемах класифікації простих задач за вихідну задачу певної групи бралася найпростіша з них, а потім складалися дві нові задачі, взаємнообернені до неї. Пропонуємо методичну роботу з кількома видами простих задач у початковому курсі математики.
Вид задачі. Задача на знаходження невідомого дільника. Задача на ділення на вміщення.
З а д а ч а. 20 кг лимонів розклали в пакети, по 4 кг у кожний. Скільки таких пакетів потрібно взяти?
Учитель пропонує викласти на парті стільки кружечків, скільки кілограмів лимонів розклали в пакети.
- Скільки кружечків викладете? (20 кружечків).
- Що означає кожний кружечок? (Кожний кружечок означає 1 кг лимонів).
- Скільки кілограмів лимонів клали в кожний пакет? (У кожний пакет клали по 4 кг лимонів).
- Розкладіть 20 кружечків у купки, по 4 кружечки в кожній.
- Скільки кружечків у кожній купці? (4 кружечки).
- Скільки отримали купок? (5 купок).
- То скільки пакетів використали для того, щоб розкласти 20 кг лимонів? (5 пакетів).
- Яку дію виконали? (Дію ділення).
- Отже, щоб знайти, скільки пакетів використали для того, щоб розкласти 20 кг лимонів, треба дізнатися, скільки разів по 4 вміщується в числі 20. Прочитайте відповідь задачі. (Використали 5 пакетів).
Запис у зошиті. 20 : 4 = 5 (п.) В і д п о в і д ь: 5 пакетів.
Вид задачі. Задача на різницеве порівняння чисел (із запитанням: "На скільки більше...?", "На скільки менше...?").
З а д а ч а. У Михайлика б зошитів у клітинку зеленого кольору і 4 зошити в лінійку синього кольору. На скільки більше зошитів у клітинку, ніж у лінійку у хлопчика?
- Що відомо в задачі? (Відомо, що в клітинку 6 зошитів).
- Що ще відомо? (У лінійку 4 зошити).
- Про що запитується в задачі? (На скільки більше зошитів у клітинку, ніж у лінійку, в Михайлика?)
Учитель відраховує 6 зошитів у клітинку зеленого кольору і 4 зошити в лінійку синього кольору. Виставляє на набірному полотні в один ряд.
Викликані учні по черзі беруть одночасно по одному зошиту зеленого і синього кольорів. Коли всі зошити парами відібрані, на набірному полотні залишилось 2 зошити зеленого кольору.
Б е с і д а в ч и т е л я.
- На скільки більше? (На 2).
- Якого кольору зошитів було менше? (Зошитів синього кольору було менше).
- На скільки менше? (На 2).
- Чому? (Бо їм не вистачило пари).
- Які зошити були зеленого кольору? (У клітинку).
- А синього? (В лінійку).
- Подивимось, скільки зошитів було в клітинку? (6).
- Скільки зошитів у лінійку? (4).
- Як отримали число 2, маючи числа 6 і 4? (Від числа 6 відняли 4).
- Отже, щоб дізнатися, на скільки зошитів у клітинку більше, ніж у лінійку і на скільки зошитів у лінійку менше, ніж у клітинку, треба від більшого числа відняти менше.
- Чому 2 зошити залишились? (Бо їх було більше).
Вид задачі. Непряма задача на віднімання (знаход¬ження меншого числа за більшим і різницею, що пока¬зує, на скільки одиниць дане число більше шуканого).
З а д а ч а. У дівчинки 6 зошитів у клітинку, що на 2 зошити більше,' ніж у лінійку. Скільки зошитів у лінійку у дівчинки?
Б е с і д а в ч и т е л я.
Б е с і д а в ч и т е л я.
- Що відомо в задачі? (Відомо, що в клітинку 6 зошитів).
- Ще що відомо? (Що їх на 2 зошити більше, ніж у лінійку).
- Про що запитується в задачі? (Скільки зошитів у лінійку?)
М і р к у в а н н я.
- Якщо в клітинку 6 зошитів і це на 2 зошити більше, ніж у лінійку, то що можна сказати про число зошитів у лінійку? (їх менше чи більше?)
- Менше. А на скільки менше? (У лінійку на 2 зошити менше).
- А якщо на 2 зошити менше, то що це означає? (Це означає, що їх стільки, скільки в клітинку, але без 2).
- То якою дією можемо дізнатися, скільки зошитів у лінійку? (Дією віднімання. Треба від числа 6 відняти 2, буде 4).
- Отже, щоб знайти менше число за більшим і різницею, що показує, на скільки одиниць дане число більше шуканого, треба виконати дію віднімання. Продовжимо роботу над даною задачею.
- Як ще можна коротко записати цю задачу? (Записати як пряму задачу).
- У клітинку — 6.
- У лінійку - ?, на 2 менше.
Якщо учень розуміє сюжет непрямої задачі і запише як пряму, то він міркує правильно.
Щоб не допустити вироблення в учнів певних штампів у міркуваннях під час розв'язування одного виду задач протягом тривалого часу, програмуй підручники побудовано так, щоб у процесі роботи над задачами одного виду учні опрацьовували задачі й інших видів, розглянуті раніше. Таке планування матеріалу ставить учнів із самого початку перед необхідністю щоразу аналізувати задачу перед тим, як вибрати ту чи іншу дію для її розв'язування.
Уже в 1 класі у зв'язку з розв'язуванням простих задач слід проводити велику узагальнювальну роботу. Розв'язуючи відповідні задачі з конкретними числовими даними, учні мають усвідомити суть дії і її застосування у вирішенні практичних завдань. Потім учитель пропонує на уроках задачі-запитання в узагальнювальній формі без конкретних даних, наприклад: "Якщо нам відомо, скільки зошитів лежить на столі в лінійку і скільки — в клітинку, то якою дією дізнаємося, скільки всього зошитів лежить на столі?". Подібні запитання ставимо на застосування кожної з інших дій. Ще більшого узагальнення набуває запис розв'язування задач у вигляді числової формули, у якій не ставлять назви при числах, що дає змогу за однією формулою складати задачі з різним конкретним змістом.
Пізніше узагальнювальні запитання слід ставити у процесі розв'язування інших видів задач, наприклад, задач на рух: "Щоб знайти швидкість потягу, що треба знати?" (Треба знати відстань, яку пройшов потяг, і час, за який потяг пройшов цю відстань). "Знаючи швидкості зустрічних поїздів і відстань між ними, що можна знайти і як?"; "У розв'язуванні задач на обчислення площ, що треба знати, щоб обчислити площу прямокутника (квадрата)?". Розв'язавши певну кількість простих задач різних видів й усвідомивши суть дій, учні зможуть дати узагальнювальні відповіді на такі запитання: "Які прості задачі розв'язуються додаванням? Відніманням? Множенням? Діленням?"
Таким чином, розв'язування арифметичних задач є не тільки важливим засобом формування в учнів математичних понять, запобігання формалізму у їх засвоєнні, а й посилює розвивальний ефект вивчення математики, впливаючи на розвиток математичного мислення учнів і їхнє оволодіння загальними прийомами міркування.
Лариса МИРОНОВСЬКА,
Ганна БОРЩ,
викладачі кафедри теорії і методики початкової освіти
Глухівського національного педагогічного університету
імені Олександра Довженка
ПОЧАТКОВА ШКОЛА
науково-методичний журнал
Ганна БОРЩ,
викладачі кафедри теорії і методики початкової освіти
Глухівського національного педагогічного університету
імені Олександра Довженка
ПОЧАТКОВА ШКОЛА
науково-методичний журнал