Мета: навчити систематизувати й групувати предмети за спільними ознаками та властивостями; застосовувати принцип доповнення та перетину множин у математичних задачах, використовуючи ідею кругів Ейлера; розвивати логічне мислення та вміння обґрунтовувати свою думку; виховувати почуття колективізму, взаємодопомоги.
Обладнання: посібник, папір та кольорові олівці, лото із зображенням тварин (свійських та диких).
Тип уроку: комбінований.
Хід уроку
І. Підготовка класу до уроку
- (Діти хором промовляють девіз уроку.)
- Часу ти не витрачай,
- Швидко логіку вивчай!
ІІ. Актуалізація опорних знань
Розумова розминка
Завдання 1 13 дітей грають у хованки. Один з них шукає, а інші — ховаються. Через певний час 9 дітей було знайдено. Скільки дітей ще ховаються? (13 – 1 - 9 = 3 дітей.)
Робота в парах
Гра «Лото» Учитель. Обговоріть у парах, на які дві групи можна поділити малюнки із зображенням тварин? (Свійські та дикі.)
Завдання 2 - Об'єднайте у групи за певними ознаками:
- 3 2 1 ?
- 8 11 +
- 5 7 III XIX
- 9 VI :
- 6 IX ІІV =
- Учитель. Скільки груп утворилось? (Відповіді учнів.)
- Учитель. Інакше ці групи можна назвати множинами. Множина—це сукупність різних об'єктів, які об'єднуються за певною спільною ознакою.
- - Як назвати першу множину? (Арабські числа.)
- - Як назвати другу множину? (Римські числа.)
- - Як назвати третю множину? (Математичні знаки.)
Завдання 3 - Обведіть лінією фігури, що мають спільну ознаку.
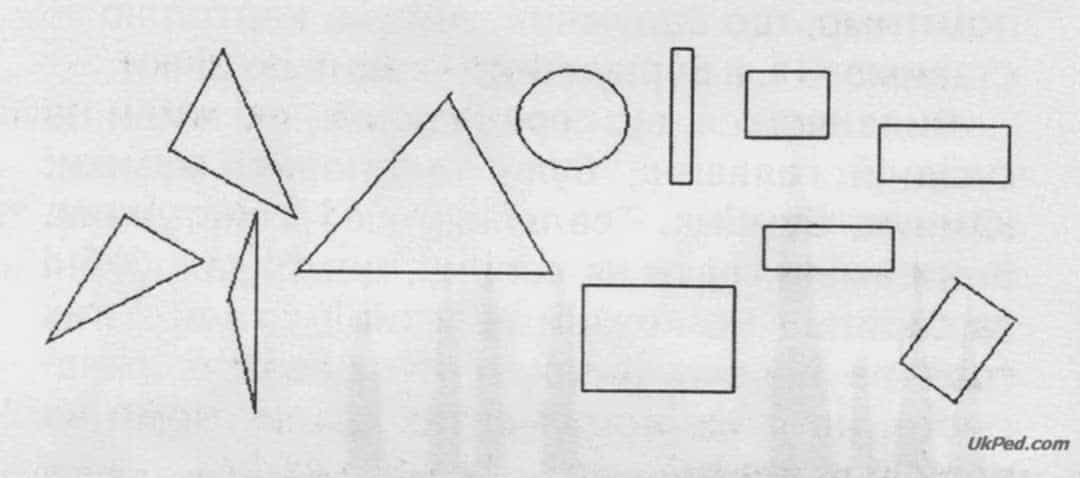
Учитель. Які множини утворилися? Що зайве? (Перша множина — трикутники; друга множина - чотирикутники; зайвим є круг.)
ІІІ. Мотивація навчальної діяльності учнів
- (Учитель повідомляє тему і мету уроку.)
- Учитель. Перший, хто запропонував об’єднувати предмети у групи за спільними ознаками, був відомий швейцарський математик — Леонард Ейлер. Ці групи зображають у формі кругів та називають кругами Ейлера.
- - Сьогодні, використовуючи ідею кругів Ейлера, ми навчимося застосовувати принцип доповнення та перетину множин у математичних задачах.
IV. Робота над матеріалом уроку
Завдання 1
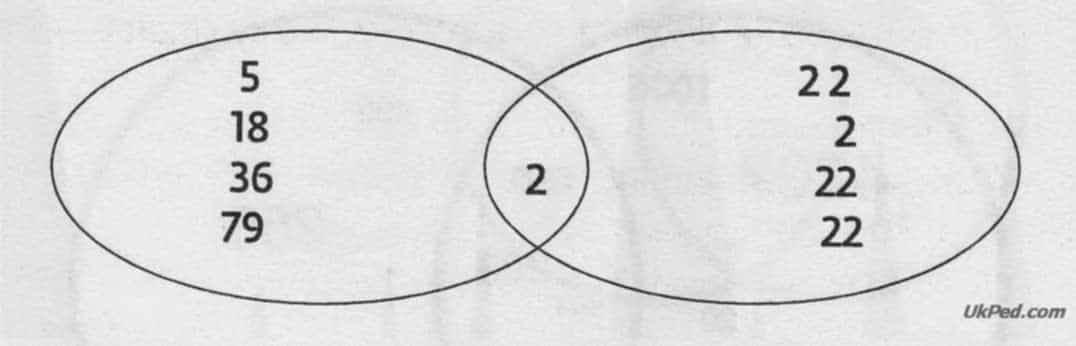
- - Що спільного між об'єктами, обведеними зеленою лінією? (Це цифри одного кольору.)
- - Що спільного між об'єктами, обведеними червоною лінією? (Усі об'єкти — цифра 2.)
- - Що утворилося на перетині цих множин? (Цифра 2 зеленого кольору.)
Завдання 2
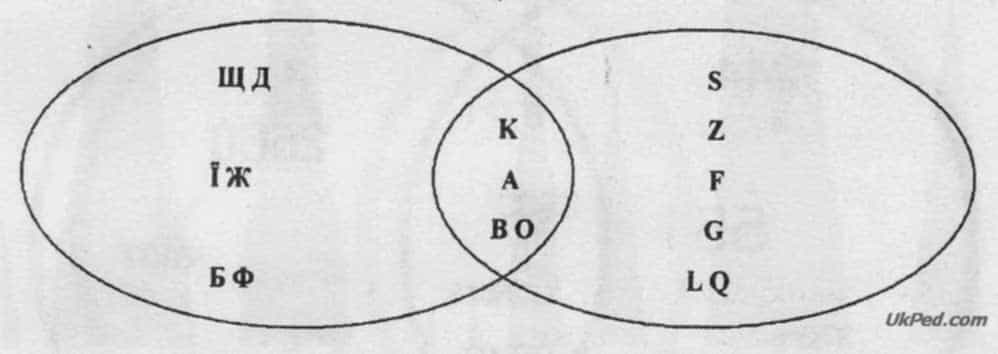
- - Що спільного між об’єктами, обведеними зеленою лінією? (Букви українського алфавіту.)
- - Що спільного між об'єктами, обведеними червоною лінією? (Букви англійського алфавіту.)
- - Що утворилося на перетині множин? (Букви, спільні для обох алфавітів.)
Робота з посібником (с. 77—80)
Завдання 1
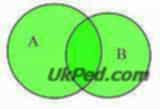
Учитель. Що спільного між фігурами, обведеними червоною лінією? А синьою? Чому деякі фігури обведені одночасно і синьою, і червоною лініями?
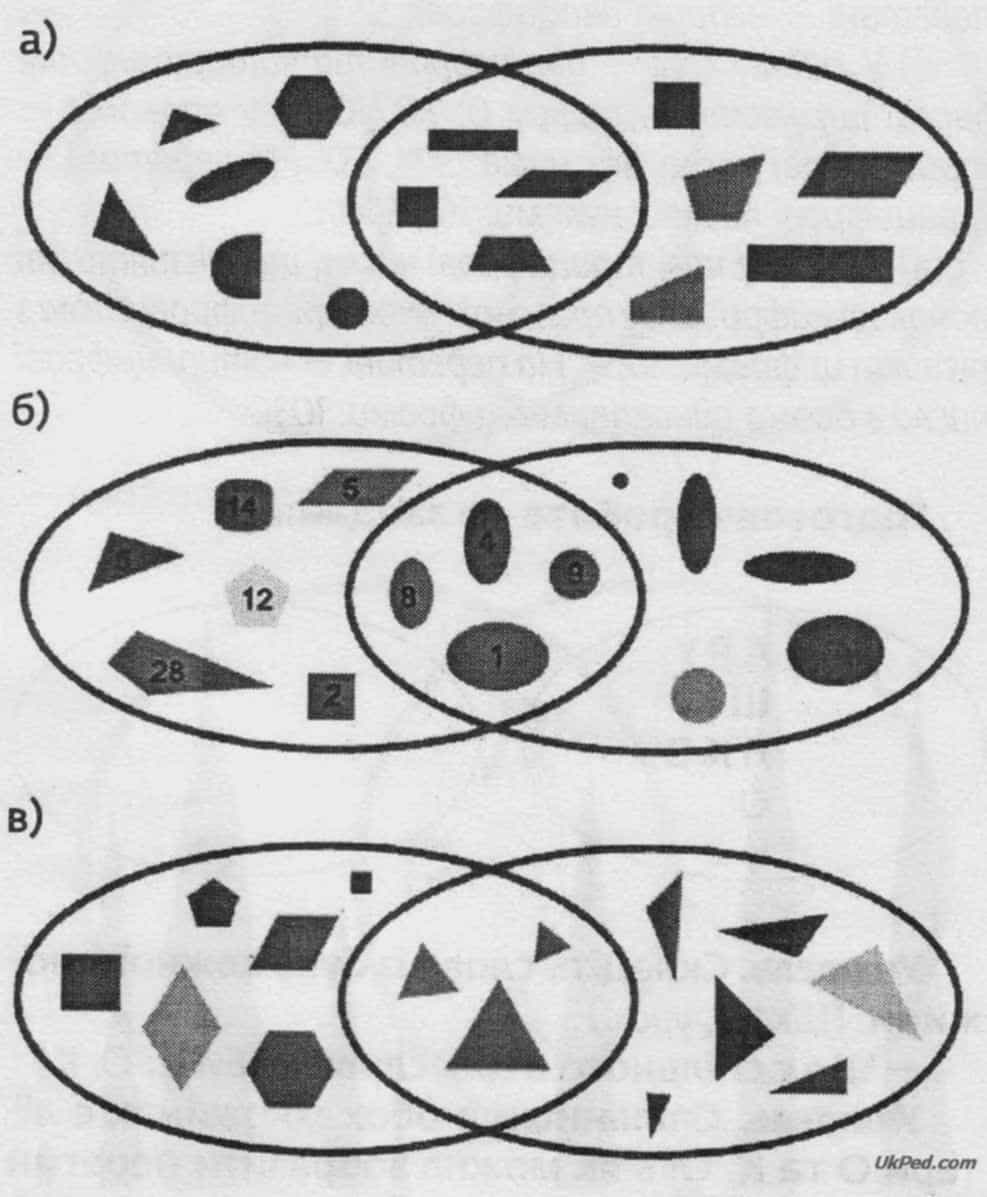
Відповіді:
- а) Червоною лінією оточені зелені фігури, синьою - чотирикутники. На перетині - зелені чотирикутники.
- б) Червоною лінією оточені фігури, що мають усередині числа, синьою — округлі фігури. На перетині — округлі фігури з числами.
- в) Червоною лінією оточені фігури, що мають рівні сторони, синьою — трикутники. На перетині — рівносторонні трикутники.
Завдання 2
Учитель. Що спільного між числами, обведеними червоною лінією? А синьою? Чому деякі числа обведені одночасно і синьою, і червоною лініями?
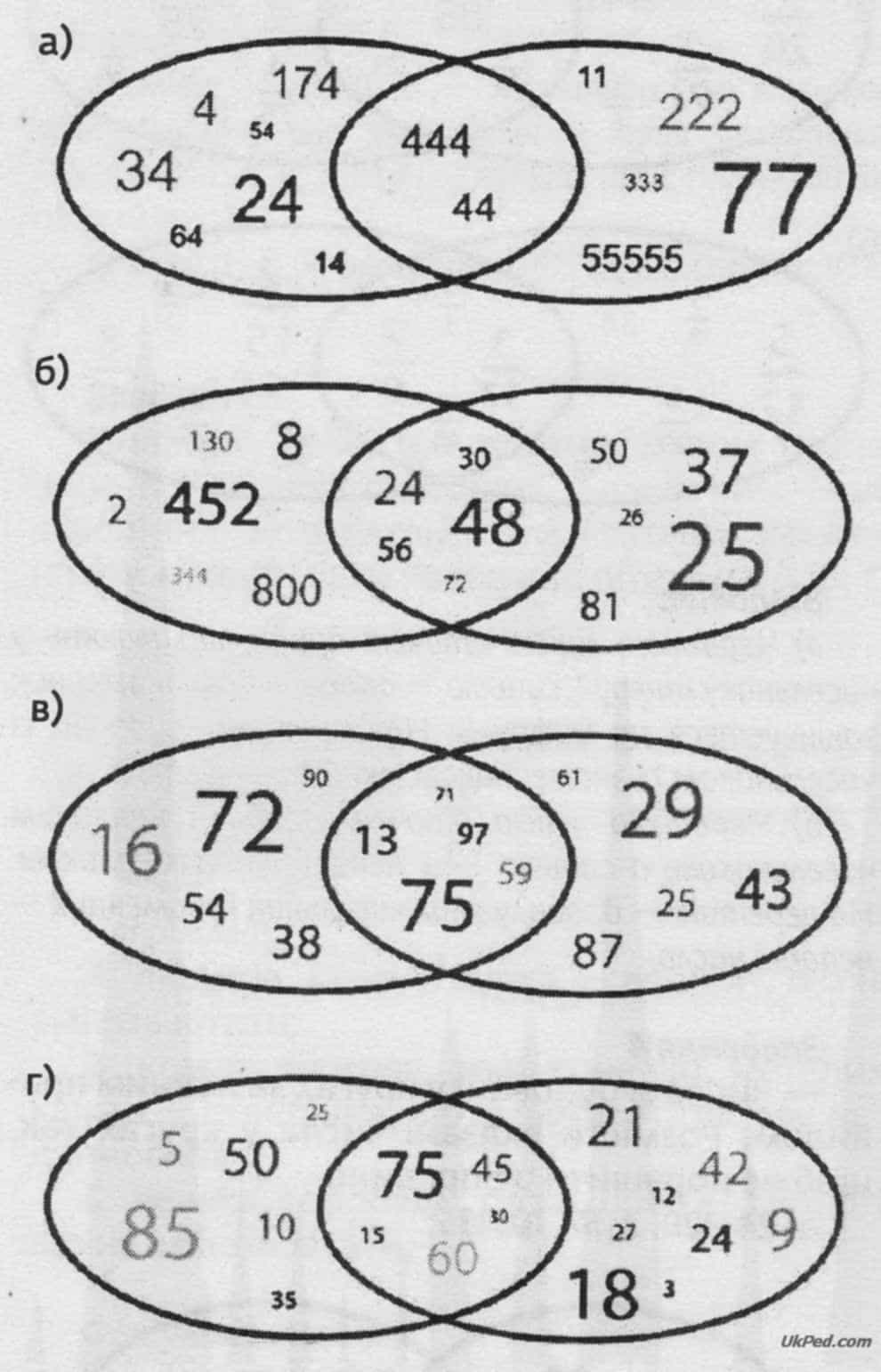
Відповіді:
- а) Червоною лінією оточені числа, що закінчуються на цифру 4, синьою — числа, що складаються з однакових цифр. На перетині — числа, що складаються з однакових цифр і закінчуються на 4, тобто лише з четвірок.
- б) Червоною лінією оточені парні числа, синьою — двоцифрові числа. На перетині — парні двоцифрові числа.
- в) Червоною лінією оточені числа, в яких перша цифра непарна, синьою — в яких друга цифра непарна. На перетині — числа, в яких перша і друга цифра непарні.
- г) Червоною лінією оточені числа, що діляться на 5, синьою — що діляться на 3. На перетині — числа, що діляться і на 5, і на 3.
Завдання 3
Учитель. Що спільного між дробами, оточеними червоною лінією? А синьою? Чому деякі дроби опинились між двома лініями?
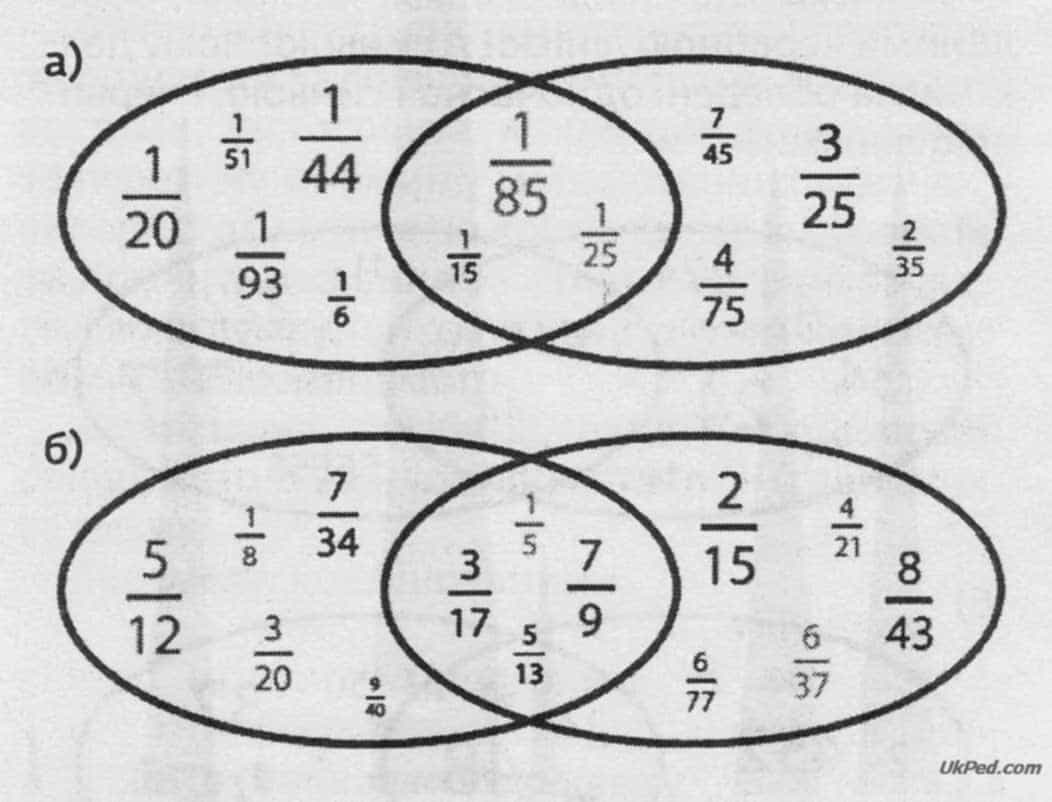
Відповіді:
- а) Червоною лінією оточені дроби, що мають у чисельнику цифру 1, синьою — дроби, в яких знаменник закінчується на цифру 5. На перетині — дроби із чисельником 1 і знаменником, який закінчується на 5.
- б) Червоною лінією оточені дроби з непарним чисельником, а синьою — з непарним знаменником. На перетині — дроби, у яких чисельник і знаменник - непарні числа.
Завдання 4
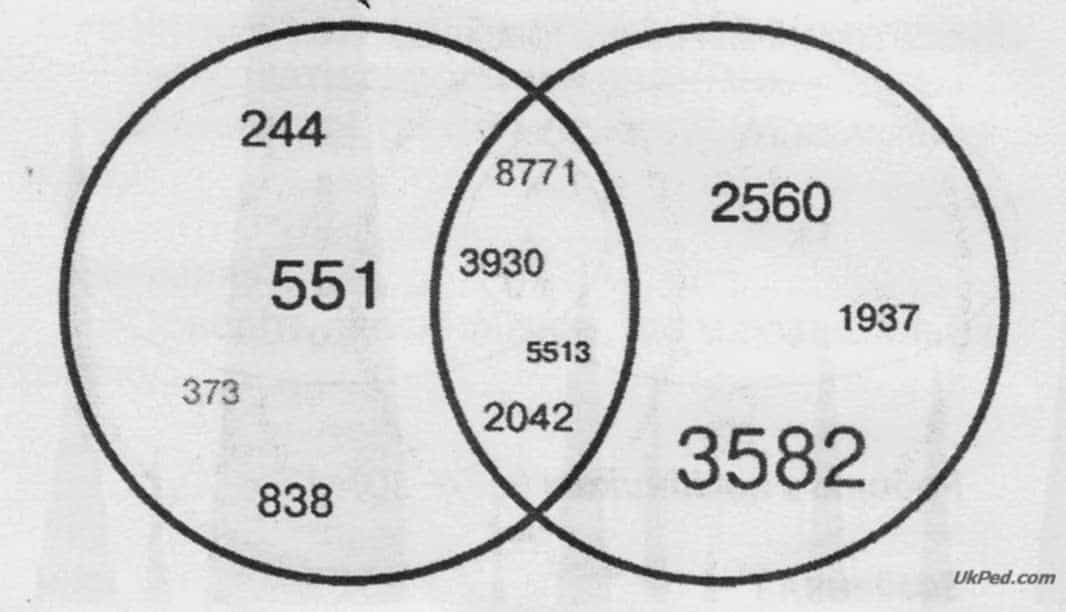
- Числа згруповані у кругах за певним правилом. Розмісти вказані числа у кругах так, щоб не порушити це правило.
а) 24, 129, 3, 57, 10, 135;
б) 924, 137, 80, 101, 1030, 540;
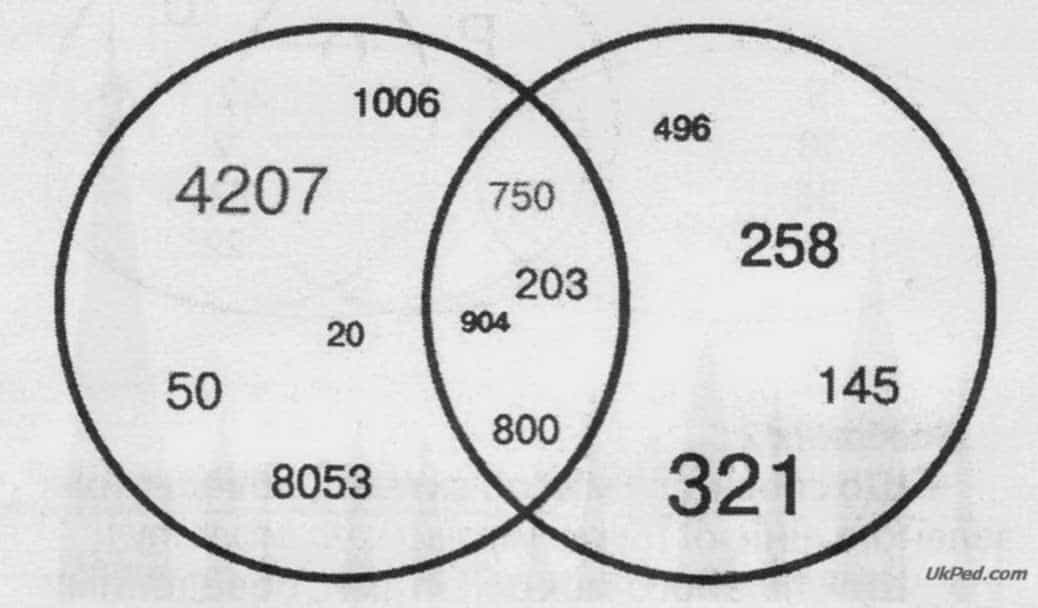
в) 9237, 101, 1030.
Відповіді:
- а) У лівому колі — двоцифрові парні числа: 24,10; у правому — одно- і трицифрові непарні: 3, 129, 135. На перетині — непарні двоцифрові: 57.
- б) У лівому колі — двоцифрові та чотирицифрові числа, що містять цифру 0: 80, 1030; у правому — трицифрові числа без нулів: 924, 137. На перетині — трицифрові числа з нулями: 101, 540.
- в) У лівому колі трицифрові числа, що містять дві однакові цифри: 101; у правому - чотирицифрові числа з різними цифрами: 9237. На перетині — чотирицифрові числа з двома однаковими цифрами: 1030.
Підготовча робота до завдання 5
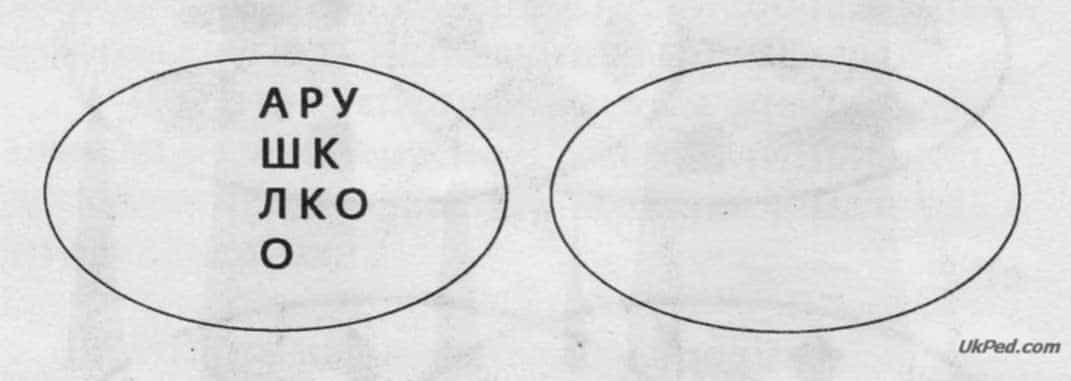
Учитель. Складіть слова із букв кожної множини. (Школа, урок.)
- Що є спільного в цих словах? (Букви О, К.)
Учитель. Спільними в обох множинах є літери О та К. Ось як можна зобразити перетин цих множин (Завдання 5, с. 80):
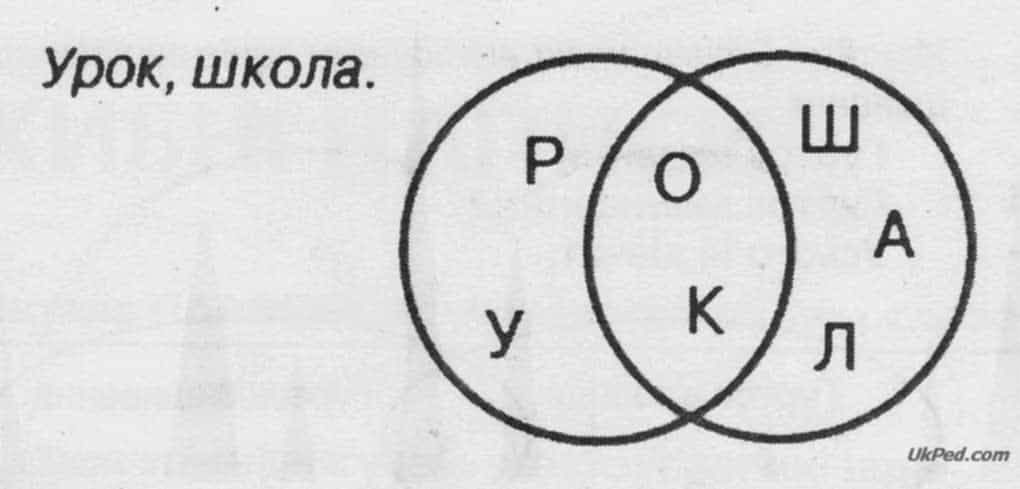
Завдання 5
Учитель. Виконай наступні завдання за цим зразком. Які літери треба поставити замість знаків питань?
а) Корова, город.
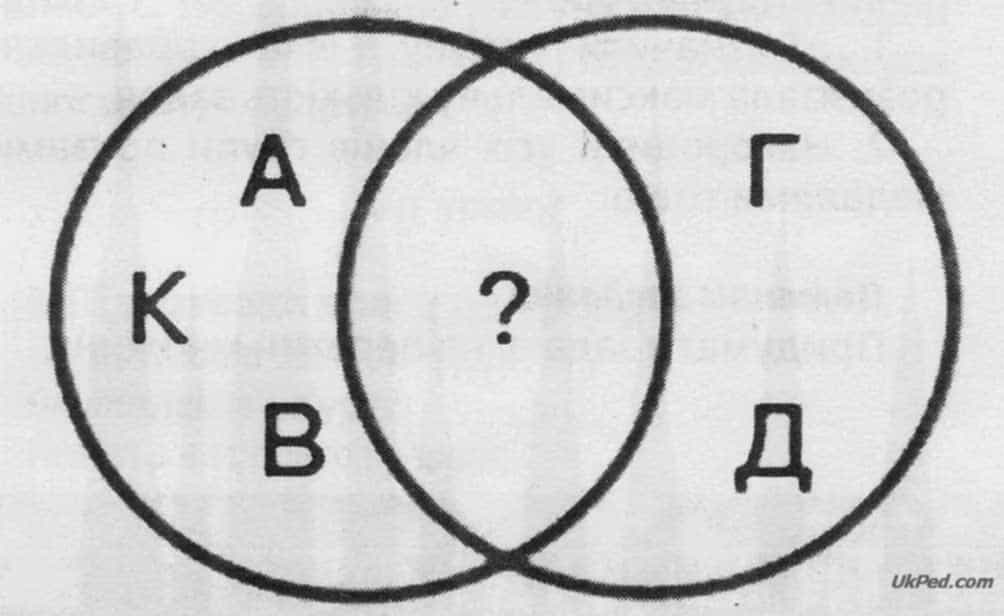
б) Комета, газета.
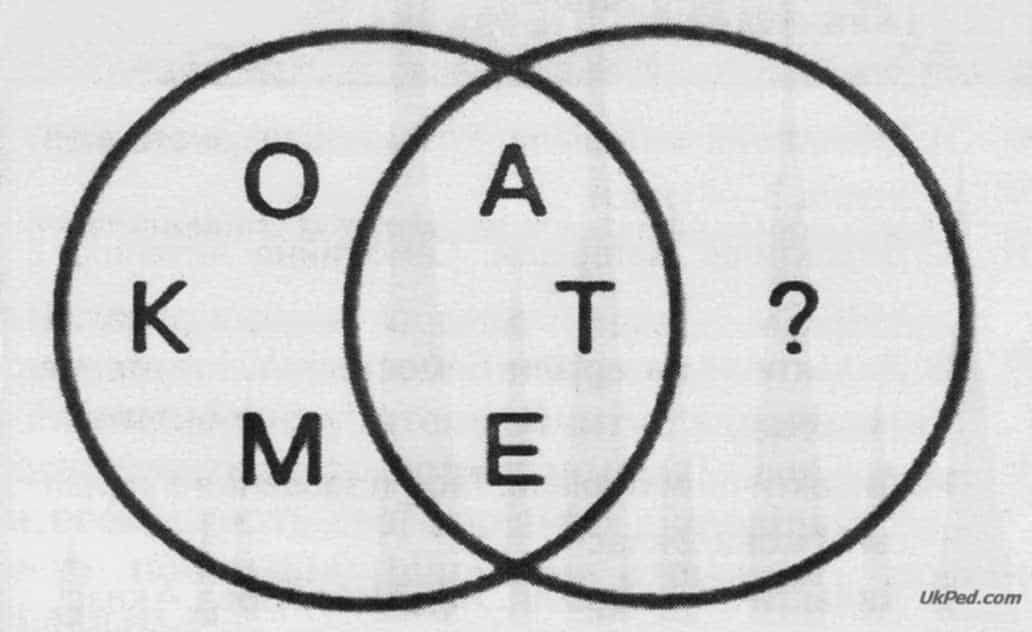
в) Град дорога
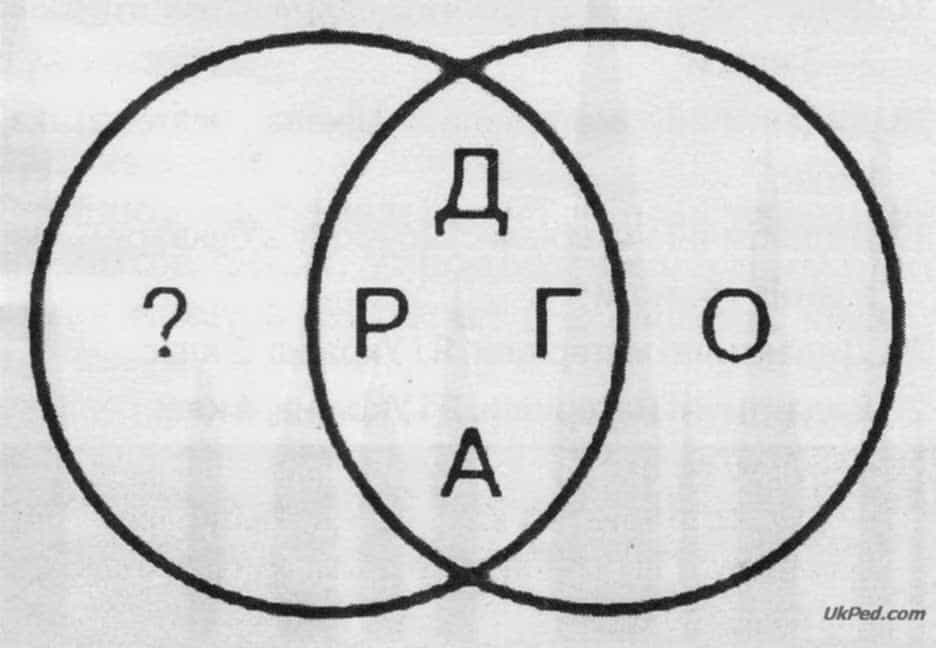
г) Умивальник, раковина,
ґ) Фотографія, автомобіль.
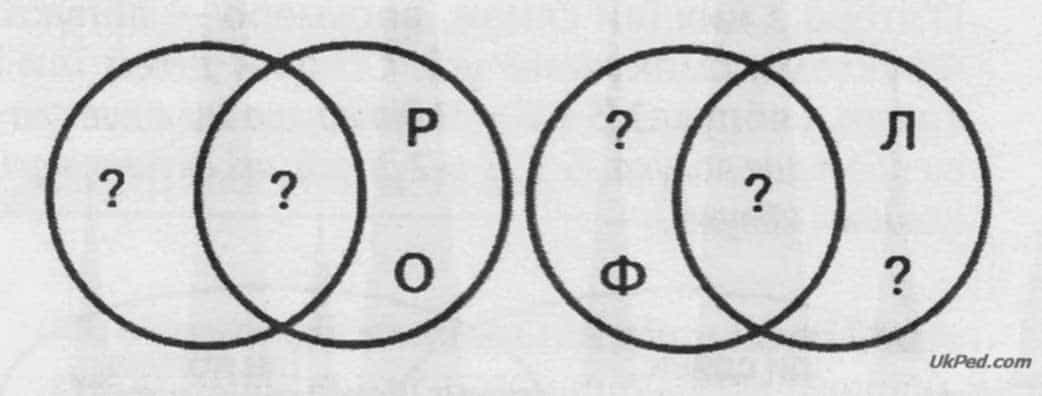
Відповіді до завдання 5:
- а) О, Р, бо це є спільні літери для слів «корова»і «город»;
- б) Г, З, бо це літери, які є у слові«газета» і яких нема у слові «комета»;
- в) нічого, бо усі літери слова «град» є у слові «дорога»;
- г) зліва: У, М, Л, Ь — ті літери, що є у слові «умивальник», але яких нема у слові «раковина». Посередині: А, В, К, И, Н — літери, що є спільними для обох слів;
- ґ) зліва: Г, Р, Я; посередині: О, Т, А, І; справа: В, М, Б, Ь.
Завдання 6
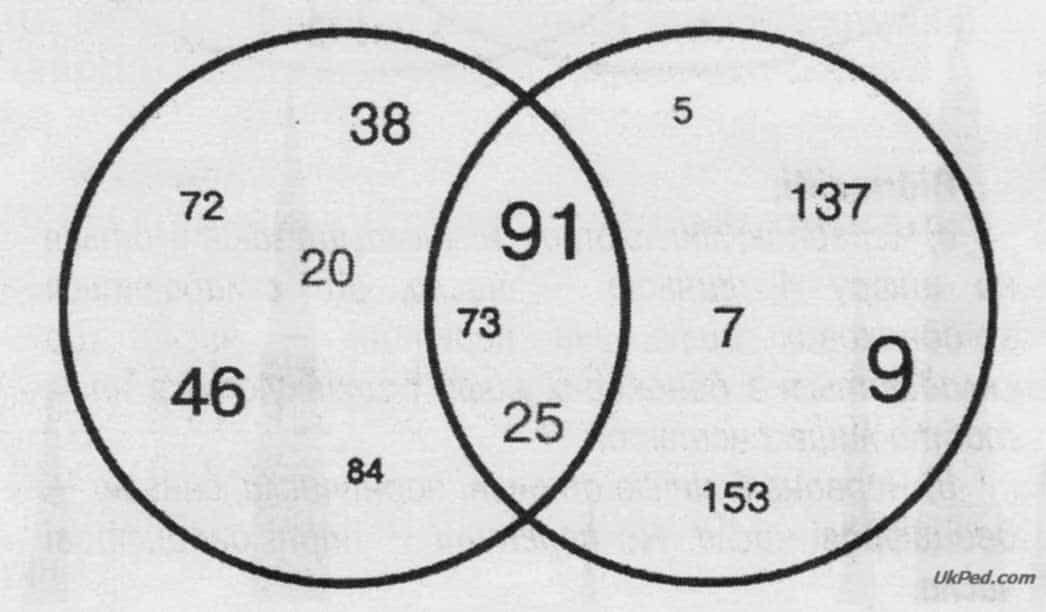
Учитель. Уяви, що жовтим колом позначено всі двоногі створіння. Блакитним — усі створіння, що вміють літати. Напиши, які живі істоти можуть бути позначені літерами А, В, С.
- А: людина, страус, курка — двоногі, що не вміють літати;
- В: комар, бджола, жук, сонечко, метелик, кажан — створіння, що вміють літати, але не є двоногими;
- С: лелека, горобець, гуска, орел — двоногі, що вміють літати.
- Фізкультхвилинка
- Раз, два, три, чотири —
- Набираємося сили.
- Нахились, повернись —
- До товариша всміхнись.
Розв'язування задач на перетин множин
Учитель. При розв’язуванні задач на перетин множин також можна застосувати круги Ейлера.
Задача 1
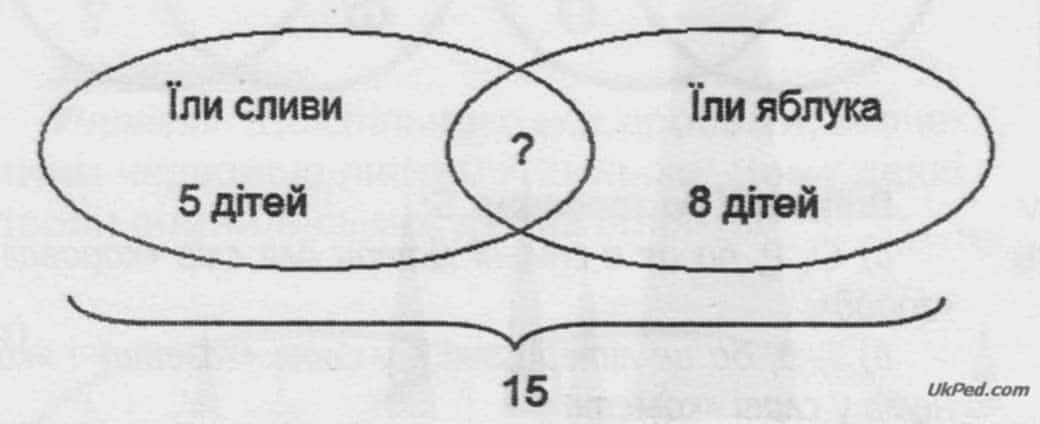
За святковим столом сиділо 15 дітей. П'ятеро з них їли сливи, восьмеро — яблука. Фруктами смакували усі. Скільки дітей їли і сливи, і яблука? (5 + 8 = 13 дітей, що їли лише сливи або лише яблука. 15 - 13 = 2 дітей, які скуштували і сливи, і яблука.)
Задача 2
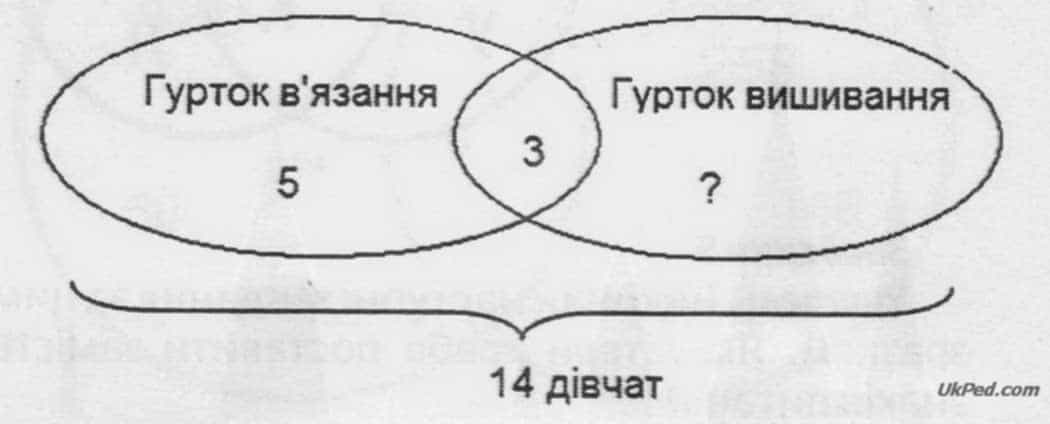
У класі навчається 14 дівчат. П'ять із них відвідують лише гурток в'язання, а три — і гурток в'язання, і гурток вишивання. Скільки дівчат відвідують лише гурток вишивання? (5 + 3 = 8 дівчат, які відвідували гурток в'язання. 14 - 8 = 6 дівчат, які відвідували лише гурток вишивання.) Гурток в’язання — 5. Гурток вишивання ? Усього 14 дівчат.
V. Підсумок уроку
1. Визначити групу, яка правильно розв'язала максимальну кількість задач.
2. Нагородити усіх членів групи призами, медалями тощо.
Домашнє завдання
Придумати задачу на перетин множин.