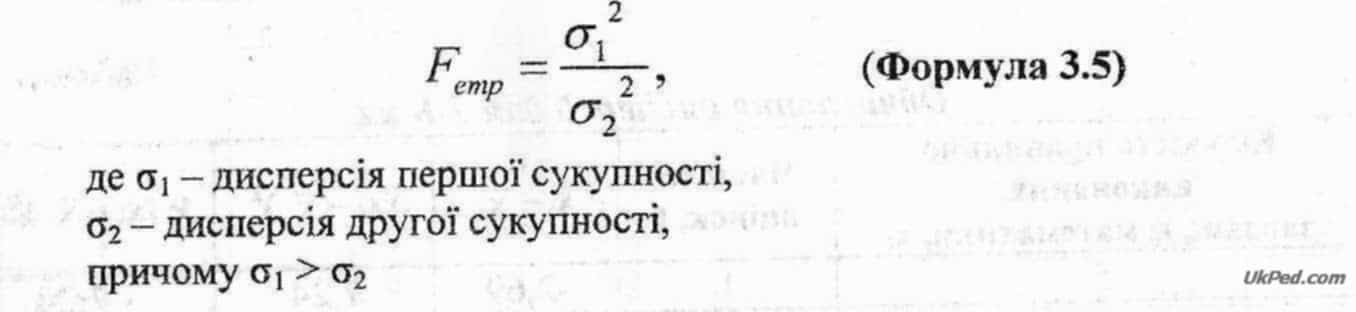Методи порівняння результатів дослідження дозволяють досліднику зробити узагальнення про однорідність вибірок (подібність чи відмінність досліджуваних класів, груп учнів тощо). У педагогіці їх найчастіше застосовують у таких випадках:
1) для порівняння контрольних і експериментальних груп, що мають бути подібними за досліджуваною ознакою, до проведення формувального етапу експерименту;
2) для визначення достовірних відмінностей між результатами контрольних та експериментальних груп після проведення формувального етапу експерименту.
Вибір методів порівняння результатів дослідження також залежить від того, за допомогою якої шкали вимірювалися значення досліджуваної ознаки. Для інтервальних шкал, якщо значення ознаки, що аналізується, розподіляються рівномірно навколо середнього арифметичного, використовують параметричні методи порівняння результатів дослідження на основі F і t критеріїв. Для порядкових шкал і нерівномірного розподілу значень доцільним є застосування непараметричного методу порівняння результатів дослідження - методу x2 (хі - квадрата). У педагогіці доцільніше користуватися непараметричним методом x2, оскільки при написанні курсових чи дипломних робіт експериментальне дослідження, як правило, проводиться на малих вибірках (від 20 до 40 учнів у класі).
Параметричні методи порівняння результатів дослідження
Використовуються для значень, отриманих у результаті вимірювання інтервальними шкалами. Ґрунтуються на порівнянні різних параметрів досліджуваних вибірок (середніх значень, дисперсій тощо).
Вибір формули обчислення 1-критерію, що служить для порівняння двох вибірок, залежить від того чи подібні ці дві групи за F-критерієм. Отже, починати порівнювати дві вибірки слід з обчислення Femp за формулою:
Дисперсія - показник, що характеризує розсіяння значень елементів сукупності (вибірки) навколо її середнього арифметичного значення. Дисперсію обчислюють за формулою:
Корінь з дисперсії називають середньоквадратичним, або стандартним відхиленням
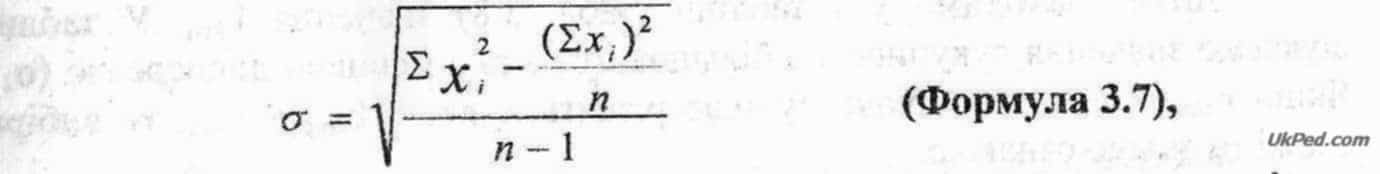
Наприклад, з'ясуємо, чи подібні два класи учнів (7-А і 7-Б) за рівнем знань з математики за F-критерієм (на основі виконання тесту). Для цього спочатку обчислимо дисперсію (б12) для першого класу (7-А) і дані занесемо до табл. 2.7, потім обчислимо дисперсію (б22) для 7-Б класу (табл. 2.8) і знайдемо Femp.
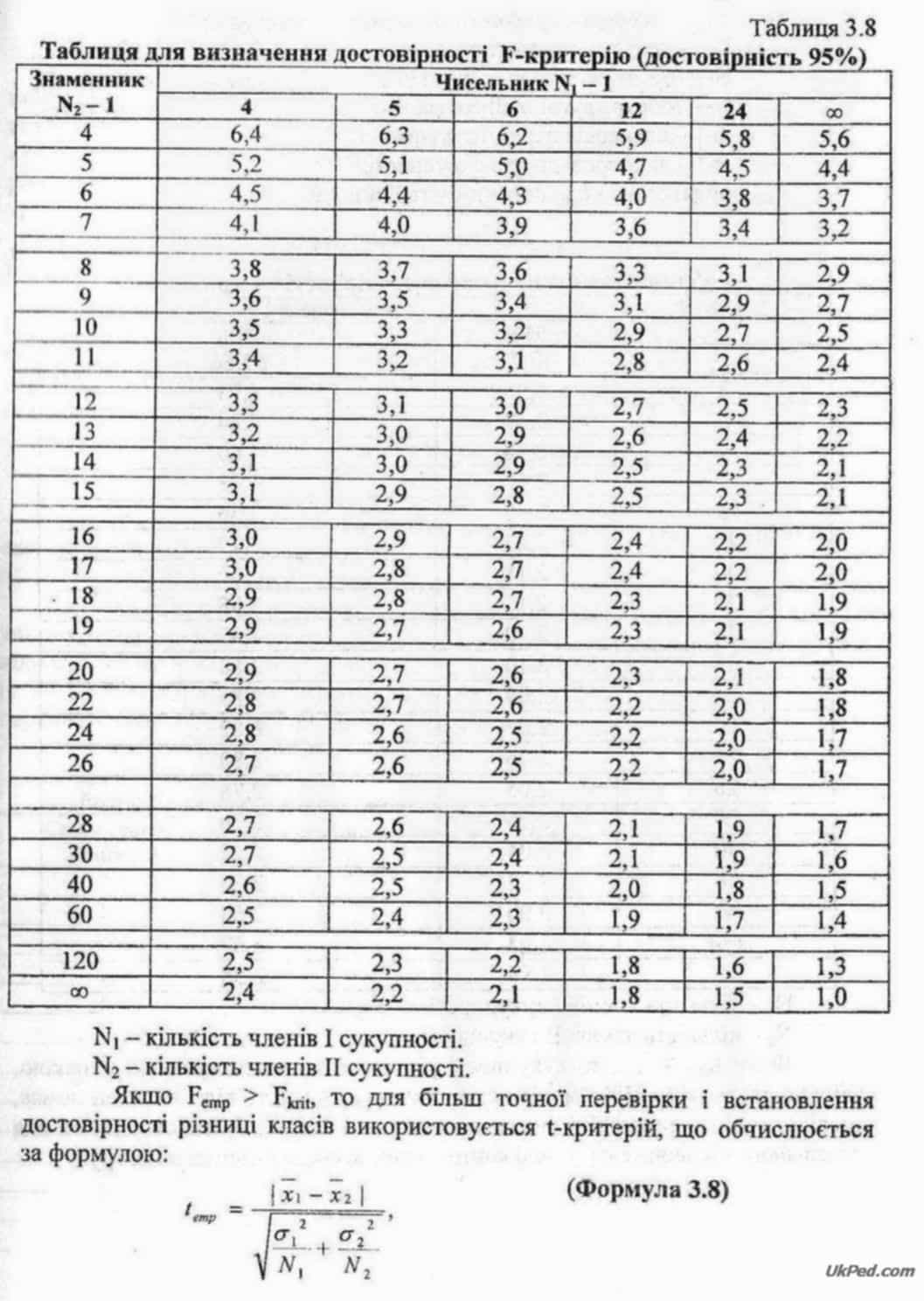
Потім знаходимо у F-таблиці (табл. 3.8) значення Fkrit У таблиці шукаємо значення сукупності з більшою (б12) та з меншою дисперсією (б22). Якщо Femp > Fkrit, то вибірки суттєво різняться, якщо Femp ? Fkrit, то вибірки схожі за даною ознакою.
У нашому прикладі Femp < Fkrit (1,65 < 1,70), отже, 7-А і 7-Б класи істотно не відрізняються за результатами своїми знаннями з математики. Вірогідність того, що ці класи подібні, складає 95%.
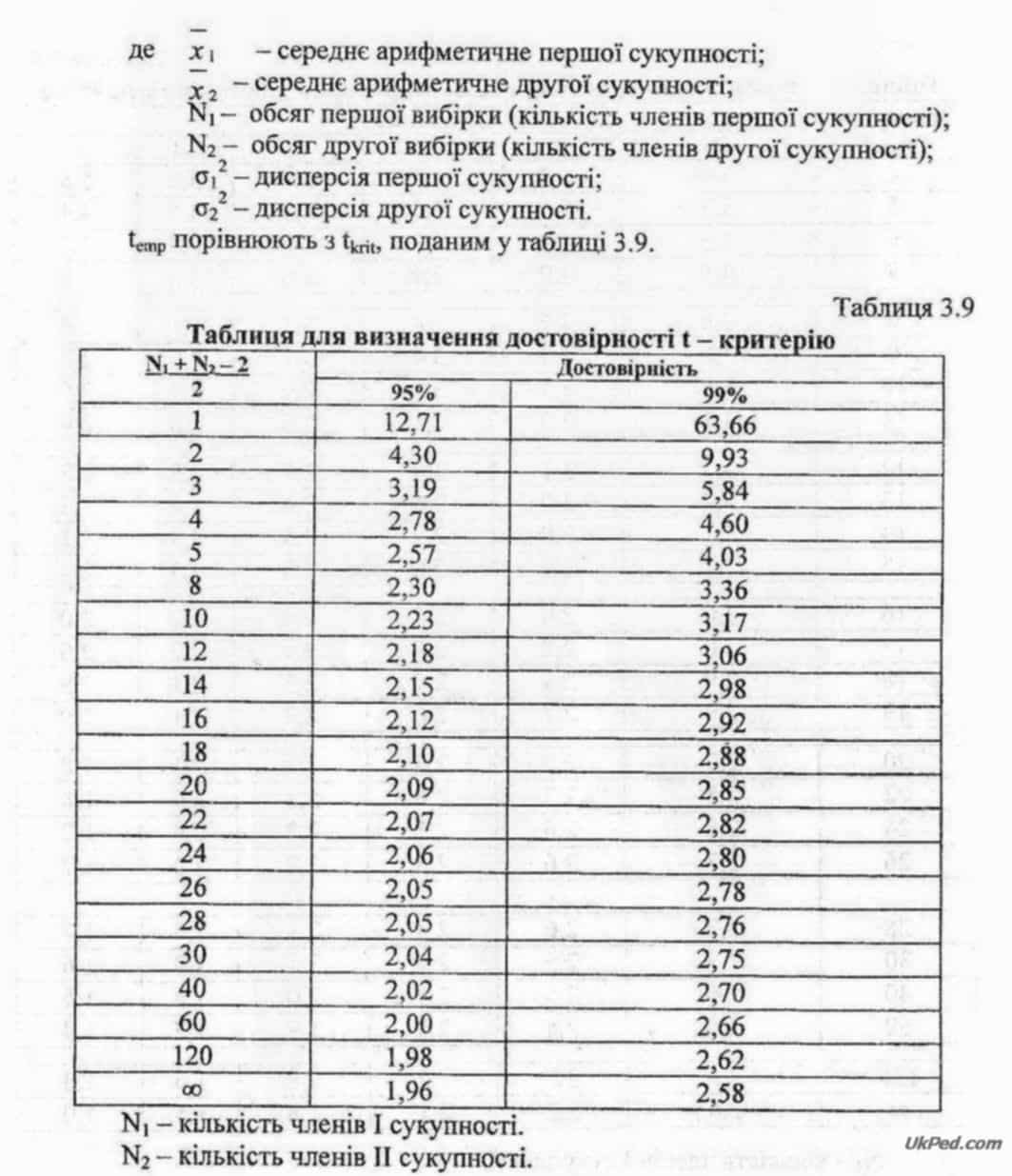
Якщо temp > tkrit, то сукупності різняться за досліджуваною ознакою, вони не однакові (з 95% ймовірністю), якщо temp ? tkrit, то відмінностей немає, досліджувані групи подібні за певною ознакою і можуть бути використані для подальшого експерименту у ролі контрольних та експериментальних груп.
Лівінський О.М., Курок О.І., Гридякін В.О., Зінченко В.П.
Методологія і методи наукових досліджень
Навчальний посібник