• Продовжити формування вмінь вирішувати завдання, використовуючи властивості квадратичної функції.
• Розвити уявлення учнів про особливості завдань, по даній темі
• Виховувати вміння слухати, аналізувати, дотримувати єдиних вимог до оформлення рішень.
Обладнання: мультимедійний проектор, екран.
Роздавальний матеріал: текст математичної вікторини, картки із графіками функцій у = х2-1 и у = 3х
Хід уроку
I. Учитель повідомляє тему уроку. За допомогою учнів формулює цілі уроку.
II. Запис домашнього завдання на наступний урок з короткими коментарями від учителя.
III. Усна робота із класом:
а) використовуючи малюнок 1, відповісти на питання:
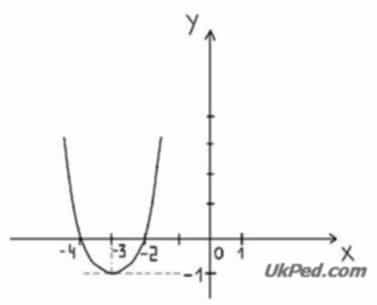
Рис. 1
1. Графік якої функції зображений на кресленні?
А. у = - (х-3)2+ 1 Б. у = (х+3)2-1 В. у = (х-1)2+3
2. Назвіть проміжки зростання й убування функції.
3. Знайдіть найбільше й найменше значення функції на [-4;-2].
4. Скільки коренів має рівняння?
А) (x+3)2-1=-5
Б) (х+3)2-1= 22
В) (х+3)2= 0
б) Математична вікторина. Учні зараховують твердження й дають їм оцінку «вірно» або «невірно»:
1. Графіком функції в=3х+2 є парабола. (Невірно)
2. (0;0)- координати вершини параболи в = х 2-2- 2 (Невірно)
3. Пряма х= 0-0- вісь симетрії параболи в = 0,5х. (Вірно)
4. Перший коефіцієнт функції в=х2+4 дорівнює 1, другий - 0, вільний член - 4. (Вірно)
5. Функція в=3х2 зростає на безлічі всіх дійсних чисел. (Невірно)
6. Галузі параболи в=-2х2+х+3 спрямовані долілиць. (Вірно)
7. У функції в=5х х-4 є найбільше значення, але немає найменшого. (Невірно)
8. Крапка В(2;-200) належить графікові функції в=-50х2. (Вірно)
9. Квадратична функція задається формулою виду в=ах2+вх+з, де а, в, з – будь-які числа. (Невірно)
10. Графік функції в=(х-1)2+2 розташований в 3-й і 4-й координатних чвертях. (Невірно)
11. Графік функції в = ах2+вх+із симетричний відносно прямій х = . (Вірно)
Робота в зошитах по домашній заготівлі графіків функцій в = 2х2+ 4х +2 і в=х+1, побудованих в одній координатній площині. Один учень викликається для роботи до дошки, де також виконана заготівля.
Завдання: використовуючи домашню заготівлю графіків функцій в=2х2+4х+2 і в=х+1, побудувати графік « кусочной» функції
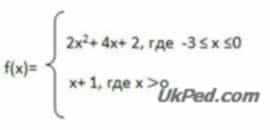
За графіком визначити область визначення, безліч значень, проміжки зростання й убування функції.
II. Закріплення алгоритму побудови графіка функції утримуючий знак модуля.
Учнем видаються картки, на яких побудовані графіки функцій у=х2-1 и у=3х..
Завдання: використовуючи графіки функцій у=х 2-1 і у=3х побудувати графіки функцій в=|3х| і в = |х2 - 1| (перевірка за графікам заздалегідь зображеним на дошці).
Диференційована самостійна робота на 15 хв (учні вибирають одне із запропонованих завдань на відповідну оцінку).
Текст роботи:
Оцінка «4»
Побудуйте графік функції у = - х2 – 6х – 5. Укажіть проміжки зростання й убування функції.
Оцінка «5»
Побудуйте графік функції у=f(x), де f(x) =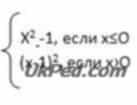
При яких значеннях х виконується нерівність у>o
Оцінка «5»
Побудуйте графік функції y=|х 2-2х-3|. Скільки загальних крапок може мати із цим графіком пряма y=1 ?
Підсумок уроку. Учні здають самостійну роботу. Учитель озвучує оцінки за урок, дякує дітям за роботу.